diff --git a/solution/0000-0099/0010.Regular Expression Matching/README.md b/solution/0000-0099/0010.Regular Expression Matching/README.md
index eb824ee89d247..5eb9ff8be6f3d 100644
--- a/solution/0000-0099/0010.Regular Expression Matching/README.md
+++ b/solution/0000-0099/0010.Regular Expression Matching/README.md
@@ -25,7 +25,7 @@ tags:
'*' 匹配零个或多个前面的那一个元素
-所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
+所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
示例 1:
diff --git a/solution/0000-0099/0075.Sort Colors/README.md b/solution/0000-0099/0075.Sort Colors/README.md
index 3cdb264d2e73e..03206a6cb6bc1 100644
--- a/solution/0000-0099/0075.Sort Colors/README.md
+++ b/solution/0000-0099/0075.Sort Colors/README.md
@@ -18,7 +18,7 @@ tags:
-给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
+给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地 对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
diff --git a/solution/0000-0099/0085.Maximal Rectangle/README.md b/solution/0000-0099/0085.Maximal Rectangle/README.md
index 8f7d6760b3a36..e549b2983cc9c 100644
--- a/solution/0000-0099/0085.Maximal Rectangle/README.md
+++ b/solution/0000-0099/0085.Maximal Rectangle/README.md
@@ -25,7 +25,7 @@ tags:
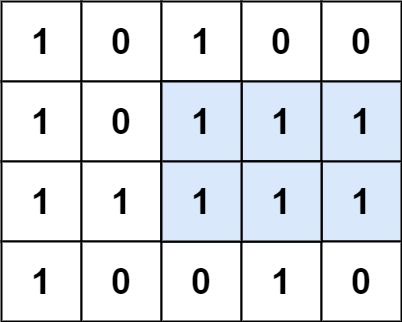
示例 1:
- +
+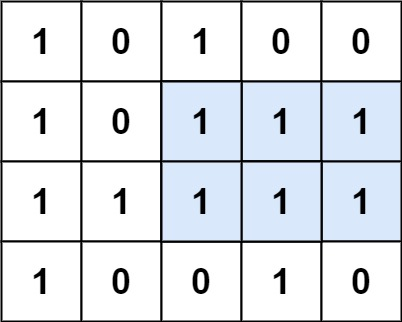
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
diff --git a/solution/0000-0099/0085.Maximal Rectangle/images/1722912576-boIxpm-image.png b/solution/0000-0099/0085.Maximal Rectangle/images/1722912576-boIxpm-image.png
new file mode 100644
index 0000000000000..bbf815c01d203
Binary files /dev/null and b/solution/0000-0099/0085.Maximal Rectangle/images/1722912576-boIxpm-image.png differ
diff --git a/solution/0200-0299/0277.Find the Celebrity/README.md b/solution/0200-0299/0277.Find the Celebrity/README.md
index 501457473064d..8ae7e2cf70159 100644
--- a/solution/0200-0299/0277.Find the Celebrity/README.md
+++ b/solution/0200-0299/0277.Find the Celebrity/README.md
@@ -18,62 +18,56 @@ tags:
-假设你是一个专业的狗仔,参加了一个 n 人派对,其中每个人被从 0 到 n - 1 标号。在这个派对人群当中可能存在一位 “名人”。所谓 “名人” 的定义是:其他所有 n - 1 个人都认识他/她,而他/她并不认识其他任何人。
+假设你是一个专业的狗仔,参加了一个 n 人派对,其中每个人被从 0 到 n - 1 标号。在这个派对人群当中可能存在一位 “名人”。所谓 “名人” 的定义是:其他所有 n - 1 个人都认识他/她,而他/她并不认识其他任何人。
-现在你想要确认这个 “名人” 是谁,或者确定这里没有 “名人”。而你唯一能做的就是问诸如 “A 你好呀,请问你认不认识 B呀?” 的问题,以确定 A 是否认识 B。你需要在(渐近意义上)尽可能少的问题内来确定这位 “名人” 是谁(或者确定这里没有 “名人”)。
+现在你想要确认这个 “名人” 是谁,或者确定这里没有 “名人”。而你唯一能做的就是问诸如 “A 你好呀,请问你认不认识 B呀?” 的问题,以确定 A 是否认识 B。你需要在(渐近意义上)尽可能少的问题内来确定这位 “名人” 是谁(或者确定这里没有 “名人”)。
-在本题中,你可以使用辅助函数 bool knows(a, b) 获取到 A 是否认识 B。请你来实现一个函数 int findCelebrity(n)。
+在本题中,你可以使用辅助函数 bool knows(a, b) 获取到 A 是否认识 B。请你来实现一个函数 int findCelebrity(n)。
-派对最多只会有一个 “名人” 参加。若 “名人” 存在,请返回他/她的编号;若 “名人” 不存在,请返回 -1。
+派对最多只会有一个 “名人” 参加。若 “名人” 存在,请返回他/她的编号;若 “名人” 不存在,请返回 -1。
-
-
-示例 1:
-
-
+
+示例 1:
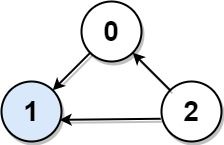
+
-输入: graph = [
- [1,1,0],
- [0,1,0],
- [1,1,1]
-]
+输入: graph = [[1,1,0],[0,1,0],[1,1,1]]
输出: 1
解释: 有编号分别为 0、1 和 2 的三个人。graph[i][j] = 1 代表编号为 i 的人认识编号为 j 的人,而 graph[i][j] = 0 则代表编号为 i 的人不认识编号为 j 的人。“名人” 是编号 1 的人,因为 0 和 2 均认识他/她,但 1 不认识任何人。
+
-示例 2:
-
-
-
+示例 2:
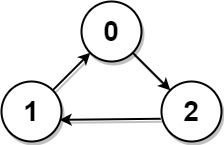
+
-输入: graph = [
- [1,0,1],
- [1,1,0],
- [0,1,1]
-]
+输入: graph = [[1,0,1],[1,1,0],[0,1,1]]
输出: -1
解释: 没有 “名人”
-
+
+
-提示:
+提示:
+
- n == graph.lengthn == graph[i].length2 <= n <= 100graph[i][j] 是 0 或 1.n == graph.length == graph[i].length2 <= n <= 100graph[i][j] 是 0 或 1graph[i][i] == 1
+
-
+
+
-进阶:如果允许调用 API knows 的最大次数为 3 * n ,你可以设计一个不超过最大调用次数的解决方案吗?
+进阶:如果允许调用 API knows 的最大次数为 3 * n ,你可以设计一个不超过最大调用次数的解决方案吗?
+
+
diff --git a/solution/0200-0299/0277.Find the Celebrity/images/277_example_1_bold.png b/solution/0200-0299/0277.Find the Celebrity/images/277_example_1_bold.png
deleted file mode 100644
index f4f70164e6181..0000000000000
Binary files a/solution/0200-0299/0277.Find the Celebrity/images/277_example_1_bold.png and /dev/null differ
diff --git a/solution/0200-0299/0277.Find the Celebrity/images/277_example_2.png b/solution/0200-0299/0277.Find the Celebrity/images/277_example_2.png
deleted file mode 100644
index 00ea91bd7a903..0000000000000
Binary files a/solution/0200-0299/0277.Find the Celebrity/images/277_example_2.png and /dev/null differ
diff --git a/solution/0500-0599/0588.Design In-Memory File System/README.md b/solution/0500-0599/0588.Design In-Memory File System/README.md
index 5d26f3be1525d..b543fc76a3ce8 100644
--- a/solution/0500-0599/0588.Design In-Memory File System/README.md
+++ b/solution/0500-0599/0588.Design In-Memory File System/README.md
@@ -7,6 +7,7 @@ tags:
- 字典树
- 哈希表
- 字符串
+ - 排序
---
diff --git a/solution/0500-0599/0588.Design In-Memory File System/README_EN.md b/solution/0500-0599/0588.Design In-Memory File System/README_EN.md
index 786d2cf8b8c43..2831cf8a0865d 100644
--- a/solution/0500-0599/0588.Design In-Memory File System/README_EN.md
+++ b/solution/0500-0599/0588.Design In-Memory File System/README_EN.md
@@ -7,6 +7,7 @@ tags:
- Trie
- Hash Table
- String
+ - Sorting
---
diff --git a/solution/0600-0699/0642.Design Search Autocomplete System/README.md b/solution/0600-0699/0642.Design Search Autocomplete System/README.md
index 4ecc38c9f5f80..3682d112a4ea2 100644
--- a/solution/0600-0699/0642.Design Search Autocomplete System/README.md
+++ b/solution/0600-0699/0642.Design Search Autocomplete System/README.md
@@ -3,6 +3,7 @@ comments: true
difficulty: 困难
edit_url: https://github.com/doocs/leetcode/edit/main/solution/0600-0699/0642.Design%20Search%20Autocomplete%20System/README.md
tags:
+ - 深度优先搜索
- 设计
- 字典树
- 字符串
diff --git a/solution/0600-0699/0642.Design Search Autocomplete System/README_EN.md b/solution/0600-0699/0642.Design Search Autocomplete System/README_EN.md
index b1c22de7dffea..362a279136264 100644
--- a/solution/0600-0699/0642.Design Search Autocomplete System/README_EN.md
+++ b/solution/0600-0699/0642.Design Search Autocomplete System/README_EN.md
@@ -3,6 +3,7 @@ comments: true
difficulty: Hard
edit_url: https://github.com/doocs/leetcode/edit/main/solution/0600-0699/0642.Design%20Search%20Autocomplete%20System/README_EN.md
tags:
+ - Depth-First Search
- Design
- Trie
- String
diff --git a/solution/0700-0799/0713.Subarray Product Less Than K/README.md b/solution/0700-0799/0713.Subarray Product Less Than K/README.md
index fae69af2d1051..9a3a24ce5353d 100644
--- a/solution/0700-0799/0713.Subarray Product Less Than K/README.md
+++ b/solution/0700-0799/0713.Subarray Product Less Than K/README.md
@@ -26,7 +26,7 @@ tags:
输入:nums = [10,5,2,6], k = 100
输出:8
-解释:8 个乘积小于 100 的子数组分别为:[10]、[5]、[2],、[6]、[10,5]、[5,2]、[2,6]、[5,2,6]。
+解释:8 个乘积小于 100 的子数组分别为:[10]、[5]、[2]、[6]、[10,5]、[5,2]、[2,6]、[5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于 100 的子数组。
diff --git a/solution/0800-0899/0840.Magic Squares In Grid/README.md b/solution/0800-0899/0840.Magic Squares In Grid/README.md
index 82b1eca486f5e..5ebc062a30c0f 100644
--- a/solution/0800-0899/0840.Magic Squares In Grid/README.md
+++ b/solution/0800-0899/0840.Magic Squares In Grid/README.md
@@ -23,6 +23,8 @@ tags:
给定一个由整数组成的row x col 的 grid,其中有多少个 3 × 3 的 “幻方” 子矩阵?(每个子矩阵都是连续的)。
+注意:虽然幻方只能包含 1 到 9 的数字,但 grid 可以包含最多15的数字。
+
示例 1:
diff --git a/solution/0800-0899/0840.Magic Squares In Grid/README_EN.md b/solution/0800-0899/0840.Magic Squares In Grid/README_EN.md
index e159a7d89cd0a..3739419c53c8b 100644
--- a/solution/0800-0899/0840.Magic Squares In Grid/README_EN.md
+++ b/solution/0800-0899/0840.Magic Squares In Grid/README_EN.md
@@ -19,9 +19,11 @@ tags:
-A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
+A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
-Given a row x col grid of integers, how many 3 x 3 "magic square" subgrids are there? (Each subgrid is contiguous).
+Given a row x col grid of integers, how many 3 x 3 contiguous magic square subgrids are there?
+
+Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.
Example 1:
diff --git a/solution/0800-0899/0898.Bitwise ORs of Subarrays/README.md b/solution/0800-0899/0898.Bitwise ORs of Subarrays/README.md
index 252448058aa7c..02bdfb7ccd11f 100644
--- a/solution/0800-0899/0898.Bitwise ORs of Subarrays/README.md
+++ b/solution/0800-0899/0898.Bitwise ORs of Subarrays/README.md
@@ -18,11 +18,11 @@ tags:
-我们有一个非负整数数组 arr 。
+给定一个整数数组 arr,返回所有 arr 的非空子数组的不同按位或的数量。
-对于每个(连续的)子数组 sub = [arr[i], arr[i + 1], ..., arr[j]] ( i <= j),我们对 sub 中的每个元素进行按位或操作,获得结果 arr[i] | arr[i + 1] | ... | arr[j] 。
+子数组的按位或是子数组中每个整数的按位或。含有一个整数的子数组的按位或就是该整数。
-返回可能结果的数量。 多次出现的结果在最终答案中仅计算一次。
+子数组 是数组内连续的非空元素序列。
@@ -61,7 +61,7 @@ tags:
1 <= nums.length <= 5 * 1040 <= nums[i] <= 1090 <= nums[i] <= 109
diff --git a/solution/0900-0999/0930.Binary Subarrays With Sum/README_EN.md b/solution/0900-0999/0930.Binary Subarrays With Sum/README_EN.md
index 1a83755d57b8e..d24e78a7fbff8 100644
--- a/solution/0900-0999/0930.Binary Subarrays With Sum/README_EN.md
+++ b/solution/0900-0999/0930.Binary Subarrays With Sum/README_EN.md
@@ -24,49 +24,32 @@ tags:
A subarray is a contiguous part of the array.
-
Example 1:
-
Input: nums = [1,0,1,0,1], goal = 2
-
Output: 4
-
Explanation: The 4 subarrays are bolded and underlined below:
-
[1,0,1,0,1]
-
[1,0,1,0,1]
-
[1,0,1,0,1]
-
[1,0,1,0,1]
-
Example 2:
-
Input: nums = [0,0,0,0,0], goal = 0
-
Output: 15
-
-
Constraints:
-
- 1 <= nums.length <= 3 * 104nums[i] is either 0 or 1.0 <= goal <= nums.length1 <= nums.length <= 3 * 104nums[i] is either 0 or 1.0 <= goal <= nums.length
diff --git a/solution/1000-1099/1002.Find Common Characters/README.md b/solution/1000-1099/1002.Find Common Characters/README.md
index 38a1ff963b4fe..8a082401a4a33 100644
--- a/solution/1000-1099/1002.Find Common Characters/README.md
+++ b/solution/1000-1099/1002.Find Common Characters/README.md
@@ -20,7 +20,7 @@ tags:
-给你一个字符串数组 words ,请你找出所有在 words 的每个字符串中都出现的共用字符( 包括重复字符),并以数组形式返回。你可以按 任意顺序 返回答案。
+给你一个字符串数组 words ,请你找出所有在 words 的每个字符串中都出现的共用字符(包括重复字符),并以数组形式返回。你可以按 任意顺序 返回答案。
diff --git a/solution/1300-1399/1395.Count Number of Teams/README.md b/solution/1300-1399/1395.Count Number of Teams/README.md
index 13ac64ce256e9..325d4a43255e1 100644
--- a/solution/1300-1399/1395.Count Number of Teams/README.md
+++ b/solution/1300-1399/1395.Count Number of Teams/README.md
@@ -6,6 +6,7 @@ rating: 1343
source: 第 182 场周赛 Q2
tags:
- 树状数组
+ - 线段树
- 数组
- 动态规划
---
diff --git a/solution/1300-1399/1395.Count Number of Teams/README_EN.md b/solution/1300-1399/1395.Count Number of Teams/README_EN.md
index 38a588c926846..60b47941ce8b1 100644
--- a/solution/1300-1399/1395.Count Number of Teams/README_EN.md
+++ b/solution/1300-1399/1395.Count Number of Teams/README_EN.md
@@ -6,6 +6,7 @@ rating: 1343
source: Weekly Contest 182 Q2
tags:
- Binary Indexed Tree
+ - Segment Tree
- Array
- Dynamic Programming
---
diff --git a/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README.md b/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README.md
index 015d48774a410..6d9f1b0bc2f0d 100644
--- a/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README.md
+++ b/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README.md
@@ -73,7 +73,7 @@ tags:
我们可以使用二维前缀和来快速计算出每个子矩形中苹果的数量,定义 $s[i][j]$ 表示矩形前 $i$ 行,前 $j$ 列的子矩形中苹果的数量,那么 $s[i][j]$ 可以由 $s[i-1][j]$, $s[i][j-1]$, $s[i-1][j-1]$ 三个子矩形的苹果数量求得,具体的计算方法如下:
$$
-s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + (pizza[i-1][j-1] == 'A')
+s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + \textit{int}(pizza[i-1][j-1] == 'A')
$$
其中 $pizza[i-1][j-1]$ 表示矩形中第 $i$ 行,第 $j$ 列的字符,如果是苹果,则为 $1$,否则为 $0$。
diff --git a/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README_EN.md b/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README_EN.md
index 1907b1f1ffcd6..236675a85adf5 100644
--- a/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README_EN.md
+++ b/solution/1400-1499/1444.Number of Ways of Cutting a Pizza/README_EN.md
@@ -69,7 +69,30 @@ tags:
-### Solution 1
+### Solution 1: 2D Prefix Sum + Memoized Search
+
+We can use a 2D prefix sum to quickly calculate the number of apples in each sub-rectangle. Define $s[i][j]$ to represent the number of apples in the sub-rectangle that includes the first $i$ rows and the first $j$ columns. Then $s[i][j]$ can be derived from the number of apples in the three sub-rectangles $s[i-1][j]$, $s[i][j-1]$, and $s[i-1][j-1]$. The specific calculation method is as follows:
+
+$$
+s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + (pizza[i-1][j-1] == 'A')
+$$
+
+Here, $pizza[i-1][j-1]$ represents the character at the $i$-th row and $j$-th column in the rectangle. If it is an apple, it is $1$; otherwise, it is $0$.
+
+Next, we design a function $dfs(i, j, k)$, which represents the number of ways to cut the rectangle $(i, j, m-1, n-1)$ with $k$ cuts to get $k+1$ pieces of pizza. Here, $(i, j)$ and $(m-1, n-1)$ are the coordinates of the top-left and bottom-right corners of the rectangle, respectively. The calculation method of the function $dfs(i, j, k)$ is as follows:
+
+- If $k = 0$, it means no more cuts can be made. We need to check if there are any apples in the rectangle. If there are apples, return $1$; otherwise, return $0$.
+- If $k \gt 0$, we need to enumerate the position of the last cut. If the last cut is horizontal, we need to enumerate the cutting position $x$, where $i \lt x \lt m$. If $s[x][n] - s[i][n] - s[x][j] + s[i][j] \gt 0$, it means there are apples in the upper piece of pizza, and we add the value of $dfs(x, j, k-1)$ to the answer. If the last cut is vertical, we need to enumerate the cutting position $y$, where $j \lt y \lt n$. If $s[m][y] - s[i][y] - s[m][j] + s[i][j] \gt 0$, it means there are apples in the left piece of pizza, and we add the value of $dfs(i, y, k-1)$ to the answer.
+
+The final answer is the value of $dfs(0, 0, k-1)$.
+
+To avoid repeated calculations, we can use memoized search. We use a 3D array $f$ to record the value of $dfs(i, j, k)$. When we need to calculate the value of $dfs(i, j, k)$, if $f[i][j][k]$ is not $-1$, it means we have already calculated it before, and we can directly return $f[i][j][k]$. Otherwise, we calculate the value of $dfs(i, j, k)$ according to the above method and save the result in $f[i][j][k]$.
+
+The time complexity is $O(m \times n \times k \times (m + n))$, and the space complexity is $O(m \times n \times k)$. Here, $m$ and $n$ are the number of rows and columns of the rectangle, respectively.
+
+Similar problems:
+
+- [2312. Selling Pieces of Wood](https://github.com/doocs/leetcode/blob/main/solution/2300-2399/2312.Selling%20Pieces%20of%20Wood/README_EN.md)
diff --git a/solution/1400-1499/1446.Consecutive Characters/README.md b/solution/1400-1499/1446.Consecutive Characters/README.md
index 49c56c0834ab5..5a5d48043ae81 100644
--- a/solution/1400-1499/1446.Consecutive Characters/README.md
+++ b/solution/1400-1499/1446.Consecutive Characters/README.md
@@ -57,11 +57,11 @@ tags:
### 方法一:遍历计数
-我们定义一个变量 $t$,表示当前连续字符的长度,初始时 $t=1$。
+我们定义一个变量 $\textit{t}$,表示当前连续字符的长度,初始时 $\textit{t}=1$。
-接下来,我们从字符串 $s$ 的第二个字符开始遍历,如果当前字符与上一个字符相同,那么 $t = t + 1$,然后更新答案 $ans = \max(ans, t)$;否则,$t = 1$。
+接下来,我们从字符串 $s$ 的第二个字符开始遍历,如果当前字符与上一个字符相同,那么 $\textit{t} = \textit{t} + 1$,然后更新答案 $\textit{ans} = \max(\textit{ans}, \textit{t})$;否则 $\textit{t} = 1$。
-最后返回答案 $ans$ 即可。
+最后返回答案 $\textit{ans}$ 即可。
时间复杂度 $O(n)$,其中 $n$ 是字符串 $s$ 的长度。空间复杂度 $O(1)$。
diff --git a/solution/1400-1499/1446.Consecutive Characters/README_EN.md b/solution/1400-1499/1446.Consecutive Characters/README_EN.md
index 8b138b4558bb4..908094f98a0e0 100644
--- a/solution/1400-1499/1446.Consecutive Characters/README_EN.md
+++ b/solution/1400-1499/1446.Consecutive Characters/README_EN.md
@@ -53,7 +53,15 @@ tags:
-### Solution 1
+### Solution 1: Traversal and Counting
+
+We define a variable $\textit{t}$ to represent the length of the current consecutive characters, initially $\textit{t}=1$.
+
+Next, we traverse the string $s$ starting from the second character. If the current character is the same as the previous character, then $\textit{t} = \textit{t} + 1$, and update the answer $\textit{ans} = \max(\textit{ans}, \textit{t})$; otherwise, set $\textit{t} = 1$.
+
+Finally, return the answer $\textit{ans}$.
+
+The time complexity is $O(n)$, where $n$ is the length of the string $s$. The space complexity is $O(1)$.
diff --git a/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README.md b/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README.md
index 1d3b75bacccac..001e7409aaf5a 100644
--- a/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README.md
+++ b/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README.md
@@ -3,6 +3,7 @@ comments: true
difficulty: 中等
edit_url: https://github.com/doocs/leetcode/edit/main/solution/1800-1899/1820.Maximum%20Number%20of%20Accepted%20Invitations/README.md
tags:
+ - 图
- 数组
- 回溯
- 矩阵
diff --git a/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README_EN.md b/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README_EN.md
index 60e153fb9c772..c78b616789c4a 100644
--- a/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README_EN.md
+++ b/solution/1800-1899/1820.Maximum Number of Accepted Invitations/README_EN.md
@@ -3,6 +3,7 @@ comments: true
difficulty: Medium
edit_url: https://github.com/doocs/leetcode/edit/main/solution/1800-1899/1820.Maximum%20Number%20of%20Accepted%20Invitations/README_EN.md
tags:
+ - Graph
- Array
- Backtracking
- Matrix
diff --git a/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/README_EN.md b/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/README_EN.md
index 6ec1f35cbc797..7b8cad13919aa 100644
--- a/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/README_EN.md
+++ b/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/README_EN.md
@@ -20,39 +20,52 @@ tags:
-There exist n rectangles in a 2D plane. You are given two 0-indexed 2D integer arrays bottomLeft and topRight, both of size n x 2, where bottomLeft[i] and topRight[i] represent the bottom-left and top-right coordinates of the ith rectangle respectively.
+There exist n rectangles in a 2D plane with edges parallel to the x and y axis. You are given two 2D integer arrays bottomLeft and topRight where bottomLeft[i] = [a_i, b_i] and topRight[i] = [c_i, d_i] represent the bottom-left and top-right coordinates of the ith rectangle, respectively.
-You can select a region formed from the intersection of two of the given rectangles. You need to find the largest area of a square that can fit inside this region if you select the region optimally.
-
-Return the largest possible area of a square, or 0 if there do not exist any intersecting regions between the rectangles.
+You need to find the maximum area of a square that can fit inside the intersecting region of at least two rectangles. Return 0 if such a square does not exist.
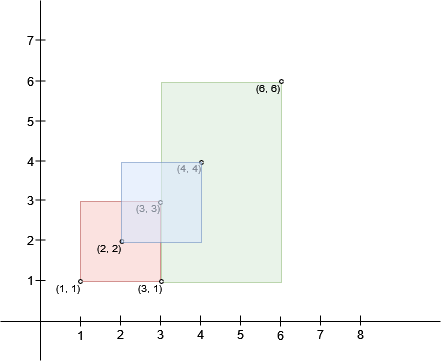
Example 1:
 -
-
-Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
-Output: 1
-Explanation: A square with side length 1 can fit inside either the intersecting region of rectangle 0 and rectangle 1, or the intersecting region of rectangle 1 and rectangle 2. Hence the largest area is side * side which is 1 * 1 == 1.
-It can be shown that a square with a greater side length can not fit inside any intersecting region.
-
+Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
+
+Output: 1
+
+Explanation:
+
+A square with side length 1 can fit inside either the intersecting region of rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the maximum area is 1. It can be shown that a square with a greater side length can not fit inside any intersecting region of two rectangles.
Example 2:
- -
-
-Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
-Output: 1
-Explanation: A square with side length 1 can fit inside either the intersecting region of rectangle 0 and rectangle 1, the intersecting region of rectangle 1 and rectangle 2, or the intersection region of all 3 rectangles. Hence the largest area is side * side which is 1 * 1 == 1.
-It can be shown that a square with a greater side length can not fit inside any intersecting region.
-Note that the region can be formed by the intersection of more than 2 rectangles.
-
+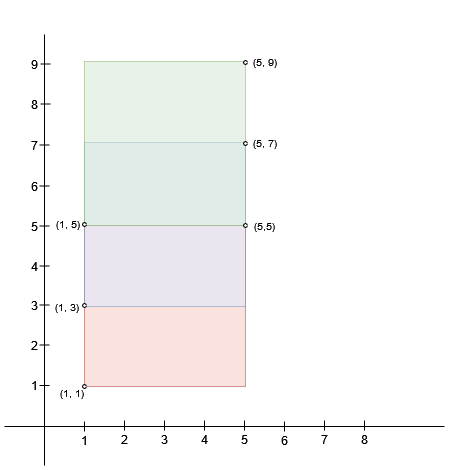 +
+Input: bottomLeft = [[1,1],[1,3],[1,5]], topRight = [[5,5],[5,7],[5,9]]
+
+Output: 4
+
+Explanation:
+
+A square with side length 2 can fit inside either the intersecting region of rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the maximum area is 2 * 2 = 4. It can be shown that a square with a greater side length can not fit inside any intersecting region of two rectangles.
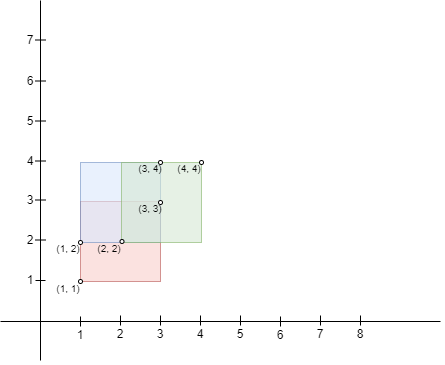
Example 3:
- -
-
-Input: bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
-Output: 0
-Explanation: No pair of rectangles intersect, hence, we return 0.
-
+ 
+
+Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
+
+Output: 1
+
+Explanation:
+
+A square with side length 1 can fit inside the intersecting region of any two rectangles. Also, no larger square can, so the maximum area is 1. Note that the region can be formed by the intersection of more than 2 rectangles.
+
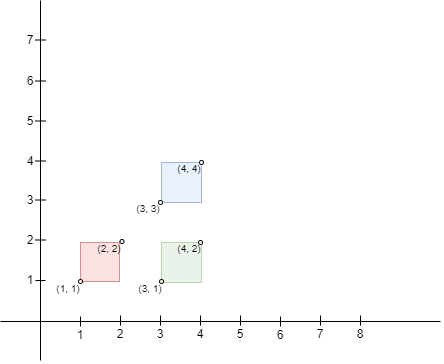
+Example 4:
+ 
+
+Input: bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
+
+Output: 0
+
+Explanation:
+
+No pair of rectangles intersect, hence, the answer is 0.
Constraints:
diff --git a/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/images/diag.png b/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/images/diag.png
new file mode 100644
index 0000000000000..886694f3a8b0d
Binary files /dev/null and b/solution/3000-3099/3047.Find the Largest Area of Square Inside Two Rectangles/images/diag.png differ
diff --git a/solution/3000-3099/3077.Maximum Strength of K Disjoint Subarrays/README_EN.md b/solution/3000-3099/3077.Maximum Strength of K Disjoint Subarrays/README_EN.md
index d8da4ba7f9d0f..5e18c7ac20f5d 100644
--- a/solution/3000-3099/3077.Maximum Strength of K Disjoint Subarrays/README_EN.md
+++ b/solution/3000-3099/3077.Maximum Strength of K Disjoint Subarrays/README_EN.md
@@ -20,40 +20,56 @@ tags:
-You are given a 0-indexed array of integers nums of length n, and a positive odd integer k.
+You are given an array of integers nums with length n, and a positive odd integer k.
-The strength of x subarrays is defined as strength = sum[1] * x - sum[2] * (x - 1) + sum[3] * (x - 2) - sum[4] * (x - 3) + ... + sum[x] * 1 where sum[i] is the sum of the elements in the ith subarray. Formally, strength is sum of (-1)i+1 * sum[i] * (x - i + 1) over all i's such that 1 <= i <= x.
+Select exactly k disjoint subarrays sub1, sub2, ..., subk from nums such that the last element of subi appears before the first element of sub{i+1} for all 1 <= i <= k-1. The goal is to maximize their combined strength.
-You need to select k disjoint subarrays from nums, such that their strength is maximum.
+The strength of the selected subarrays is defined as:
-Return the maximum possible strength that can be obtained.
+strength = k * sum(sub1)- (k - 1) * sum(sub2) + (k - 2) * sum(sub3) - ... - 2 * sum(sub{k-1}) + sum(subk)
-Note that the selected subarrays don't need to cover the entire array.
+where sum(subi) is the sum of the elements in the i-th subarray.
+
+Return the maximum possible strength that can be obtained from selecting exactly k disjoint subarrays from nums.
+
+Note that the chosen subarrays don't need to cover the entire array.
Example 1:
-
-Input: nums = [1,2,3,-1,2], k = 3
-Output: 22
-Explanation: The best possible way to select 3 subarrays is: nums[0..2], nums[3..3], and nums[4..4]. The strength is (1 + 2 + 3) * 3 - (-1) * 2 + 2 * 1 = 22.
-
+Input: nums = [1,2,3,-1,2], k = 3
+
+Output: 22
+
+Explanation:
+
+The best possible way to select 3 subarrays is: nums[0..2], nums[3..3], and nums[4..4]. The strength is calculated as follows:
+
+strength = 3 * (1 + 2 + 3) - 2 * (-1) + 2 = 22
+
+
Example 2:
-
-Input: nums = [12,-2,-2,-2,-2], k = 5
-Output: 64
-Explanation: The only possible way to select 5 disjoint subarrays is: nums[0..0], nums[1..1], nums[2..2], nums[3..3], and nums[4..4]. The strength is 12 * 5 - (-2) * 4 + (-2) * 3 - (-2) * 2 + (-2) * 1 = 64.
-
+Input: nums = [12,-2,-2,-2,-2], k = 5
+
+Output: 64
+
+Explanation:
+
+The only possible way to select 5 disjoint subarrays is: nums[0..0], nums[1..1], nums[2..2], nums[3..3], and nums[4..4]. The strength is calculated as follows:
+
+strength = 5 * 12 - 4 * (-2) + 3 * (-2) - 2 * (-2) + (-2) = 64
Example 3:
-
-Input: nums = [-1,-2,-3], k = 1
-Output: -1
-Explanation: The best possible way to select 1 subarray is: nums[0..0]. The strength is -1.
-
+Input: nums = [-1,-2,-3], k = 1
+
+Output: -1
+
+Explanation:
+
+The best possible way to select 1 subarray is: nums[0..0]. The strength is -1.
Constraints:
diff --git a/solution/3100-3199/3145.Find Products of Elements of Big Array/README.md b/solution/3100-3199/3145.Find Products of Elements of Big Array/README.md
index e405d5ea39535..4d89e50ccc1d1 100644
--- a/solution/3100-3199/3145.Find Products of Elements of Big Array/README.md
+++ b/solution/3100-3199/3145.Find Products of Elements of Big Array/README.md
@@ -20,9 +20,46 @@ tags:
-一个整数 x 的 强数组 指的是满足和为 x 的二的幂的最短有序数组。比方说,11 的强数组为 [1, 2, 8] 。
+一个非负整数 x 的 强数组 指的是满足元素为 2 的幂且元素总和为 x 的最短有序数组。下表说明了如何确定 强数组 的示例。可以证明,x 对应的强数组是独一无二的。
+
+
+
+
+ | 数字 |
+ 二进制表示 |
+ 强数组 |
+
+
+ | 1 |
+ 00001 |
+ [1] |
+
+
+ | 8 |
+ 01000 |
+ [8] |
+
+
+ | 10 |
+ 01010 |
+ [2, 8] |
+
+
+ | 13 |
+ 01101 |
+ [1, 4, 8] |
+
+
+ | 23 |
+ 10111 |
+ [1, 2, 4, 16] |
+
+
+
-我们将每一个正整数 i (即1,2,3等等)的 强数组 连接得到数组 big_nums ,big_nums 开始部分为 [1, 2, 1, 2, 4, 1, 4, 2, 4, 1, 2, 4, 8, ...] 。
+
+
+我们将每一个升序的正整数 i (即1,2,3等等)的 强数组 连接得到数组 big_nums ,big_nums 开始部分为 [1, 2, 1, 2, 4, 1, 4, 2, 4, 1, 2, 4, 8, ...] 。
给你一个二维整数数组 queries ,其中 queries[i] = [fromi, toi, modi] ,你需要计算 (big_nums[fromi] * big_nums[fromi + 1] * ... * big_nums[toi]) % modi 。
@@ -30,35 +67,31 @@ tags:
-示例 1:
+示例 1:
-
-
输入:queries = [[1,3,7]]
+
输入:queries = [[1,3,7]]
-
输出:[4]
+
输出:[4]
解释:
只有一个查询。
-
big_nums[1..3] = [2,1,2] 。它们的乘积为 4 ,4 对 7 取余数得到 4 。
-
big_nums[1..3] = [2,1,2] 。它们的乘积为 4。结果为 4 % 7 = 4。
-示例 2:
+示例 2:
-
-
输入:queries = [[2,5,3],[7,7,4]]
+
输入:queries = [[2,5,3],[7,7,4]]
-
输出:[2,2]
+
输出:[2,2]
解释:
有两个查询。
-
第一个查询:big_nums[2..5] = [1,2,4,1] 。它们的乘积为 8 ,8 对 3 取余数得到 2 。
+
第一个查询:big_nums[2..5] = [1,2,4,1] 。它们的乘积为 8 。结果为 8 % 3 = 2。
-
第二个查询:big_nums[7] = 2 ,2 对 4 取余数得到 2 。
-
第二个查询:big_nums[7] = 2 。结果为 2 % 4 = 2。
@@ -71,6 +104,8 @@ tags:
1 <= queries[i][2] <= 105
+
+
## 解法
diff --git a/solution/3100-3199/3145.Find Products of Elements of Big Array/README_EN.md b/solution/3100-3199/3145.Find Products of Elements of Big Array/README_EN.md
index 381c10968c8a9..381aec84bfd43 100644
--- a/solution/3100-3199/3145.Find Products of Elements of Big Array/README_EN.md
+++ b/solution/3100-3199/3145.Find Products of Elements of Big Array/README_EN.md
@@ -20,9 +20,44 @@ tags:
-A powerful array for an integer x is the shortest sorted array of powers of two that sum up to x. For example, the powerful array for 11 is [1, 2, 8].
-
-The array big_nums is created by concatenating the powerful arrays for every positive integer i in ascending order: 1, 2, 3, and so forth. Thus, big_nums starts as [1, 2, 1, 2, 4, 1, 4, 2, 4, 1, 2, 4, 8, ...].
+The powerful array of a non-negative integer x is defined as the shortest sorted array of powers of two that sum up to x. The table below illustrates examples of how the powerful array is determined. It can be proven that the powerful array of x is unique.
+
+
+
+
+ | num |
+ Binary Representation |
+ powerful array |
+
+
+ | 1 |
+ 00001 |
+ [1] |
+
+
+ | 8 |
+ 01000 |
+ [8] |
+
+
+ | 10 |
+ 01010 |
+ [2, 8] |
+
+
+ | 13 |
+ 01101 |
+ [1, 4, 8] |
+
+
+ | 23 |
+ 10111 |
+ [1, 2, 4, 16] |
+
+
+
+
+The array big_nums is created by concatenating the powerful arrays for every positive integer i in ascending order: 1, 2, 3, and so on. Thus, big_nums begins as [1, 2, 1, 2, 4, 1, 4, 2, 4, 1, 2, 4, 8, ...].
You are given a 2D integer matrix queries, where for queries[i] = [fromi, toi, modi] you should calculate (big_nums[fromi] * big_nums[fromi + 1] * ... * big_nums[toi]) % modi.
@@ -40,7 +75,7 @@ tags:
There is one query.
-big_nums[1..3] = [2,1,2]. The product of them is 4. The remainder of 4 under 7 is 4.
+big_nums[1..3] = [2,1,2]. The product of them is 4. The result is 4 % 7 = 4.
Example 2:
@@ -54,9 +89,9 @@ tags:
There are two queries.
-First query: big_nums[2..5] = [1,2,4,1]. The product of them is 8. The remainder of 8 under 3 is 2.
+First query: big_nums[2..5] = [1,2,4,1]. The product of them is 8. The result is 8 % 3 = 2.
-Second query: big_nums[7] = 2. The remainder of 2 under 4 is 2.
+Second query: big_nums[7] = 2. The result is 2 % 4 = 2.
diff --git a/solution/3200-3299/3237.Alt and Tab Simulation/README.md b/solution/3200-3299/3237.Alt and Tab Simulation/README.md
index 21ead8c7f193e..6f3581ae4ecf7 100644
--- a/solution/3200-3299/3237.Alt and Tab Simulation/README.md
+++ b/solution/3200-3299/3237.Alt and Tab Simulation/README.md
@@ -22,7 +22,7 @@ tags:
给定数组 windows 包含窗口的初始顺序(第一个元素在最前面,最后一个元素在最后面)。
-同时给定数组 queries 表示每一次查询中,窗口 queries[i] 被切换到最前面。
+同时给定数组 queries 表示每一次查询中,编号为 queries[i] 的窗口被切换到最前面。
返回 windows 数组的最后状态。
diff --git a/solution/3200-3299/3246.Premier League Table Ranking/README.md b/solution/3200-3299/3246.Premier League Table Ranking/README.md
index 944dc9f5d26ce..5d3e6ec2c5ab8 100644
--- a/solution/3200-3299/3246.Premier League Table Ranking/README.md
+++ b/solution/3200-3299/3246.Premier League Table Ranking/README.md
@@ -33,7 +33,7 @@ team_id 是这张表的唯一主键。
这张表包含队伍 id,队伍名,场次,赢局,平局和输局。
-编写一个解决方啊来计算联盟中每支球队的 得分 和 排名。积分计算方式如下:
+编写一个解决方案来计算联盟中每支球队的 得分 和 排名。积分计算方式如下:
- 赢局 有
3 点得分
diff --git a/solution/3200-3299/3247.Number of Subsequences with Odd Sum/README.md b/solution/3200-3299/3247.Number of Subsequences with Odd Sum/README.md
index b094d2203a0dc..ac085fbbc3384 100644
--- a/solution/3200-3299/3247.Number of Subsequences with Odd Sum/README.md
+++ b/solution/3200-3299/3247.Number of Subsequences with Odd Sum/README.md
@@ -6,7 +6,7 @@ edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3247.Nu
-# [3247. Number of Subsequences with Odd Sum 🔒](https://leetcode.cn/problems/number-of-subsequences-with-odd-sum)
+# [3247. 奇数和子序列的数量 🔒](https://leetcode.cn/problems/number-of-subsequences-with-odd-sum)
[English Version](/solution/3200-3299/3247.Number%20of%20Subsequences%20with%20Odd%20Sum/README_EN.md)
@@ -14,37 +14,39 @@ edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3247.Nu
-Given an array nums, return the number of subsequences with an odd sum of elements.
+给定一个数组 nums,返回元素和为奇数的 子序列 的数量。
-Since the answer may be very large, return it modulo 109 + 7.
+由于答案可能很大,返回答案对 109 + 7 取模。
-Example 1:
+
+示例 1:
-
Input: nums = [1,1,1]
+
输入:nums = [1,1,1]
-
Output: 4
+
输出:4
-
Explanation:
+
解释:
-
The odd-sum subsequences are: [1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1].
+
奇数和子序列为:[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1].
Example 2:
+示例 2:
-
Input: nums = [1,2,2]
+
输入:nums = [1,2,2]
-
Output: 4
+
输出:4
-
Explanation:
+
解释:
-
The odd-sum subsequences are: [1, 2, 2], [1, 2, 2], [1, 2, 2], [1, 2, 2].
+
奇数和子序列为:[1, 2, 2], [1, 2, 2], [1, 2, 2], [1, 2, 2].
-Constraints:
+
+提示:
1 <= nums.lnegth <= 105




 +
+
 -
- -
- +
+ -
-