Vector circle-square mapping methods #95
Description
I just found this repo. My personal vector helper class has the following functions that could be useful to others.
The controllers in Godot give you a value from -1 to 1 for both the x and y. Some math operations require a more normalized version of the input, but just doing vector.normalized() chops the vector short instead of properly scaling it. In other words, you get this:
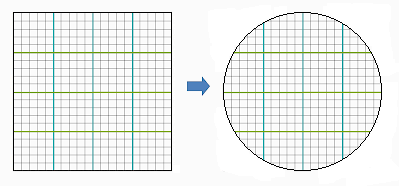
The more proper way to do it and eliminate these "dead zones" in the corners, is to map the square space to a circle space.
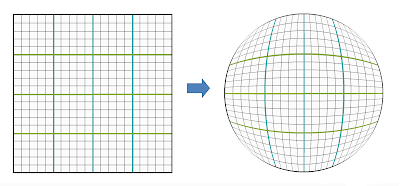
Inversely, mapping the circle-based normals to a square would look like this:
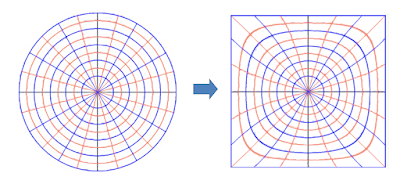
For a bit more info on the math, this blog post does an ok job explaining: http://squircular.blogspot.com/2015/09/mapping-circle-to-square.html
Below is my implementation. Feel free to tweak it to make it faster.
const __2root2 := 2.0 * sqrt(2.0)
# Map a circle grid to a square grid
# input: vector from a circular domain with radius of 1
# output: vector in a square domain from (-1,-1) to (1,1)
static func map_circle_to_square( xy :Vector2 ) -> Vector2:
var x2 := xy[0]*xy[0]
var y2 := xy[1]*xy[1]
return Vector2(
0.5 * (sqrt(2.0 + x2 - y2 + xy[0] * __2root2) - sqrt(2.0 + x2 - y2 - xy[0] * __2root2)),
0.5 * (sqrt(2.0 - x2 + y2 + xy[1] * __2root2) - sqrt(2.0 - x2 + y2 - xy[1] * __2root2))
)
# Map a square grid to a circular grid
# input: vector from a square domain from (-1,-1) to (1,1)
# output: vector in a circle domain with radius of 1
static func map_square_to_circle( xy :Vector2 ) -> Vector2:
return Vector2(
xy.x * sqrt(1.0 - xy.y*xy.y/2.0),
xy.y * sqrt(1.0 - xy.x*xy.x/2.0)
)Also, if this doesn't seem useful to anyone else, feel free to scrap this issue. I just know these took me a long time to find and figure out.