Skip to content
This repository was archived by the owner on Mar 28, 2023. It is now read-only.

Latest commit

 

History

History
113 lines (68 loc) · 8.67 KB

statistical_model.md

File metadata and controls

113 lines (68 loc) · 8.67 KB

Table of contents

  1. Sat-to-Ground (and vice versa) link budget calculation
  2. Intersatellite Link budget calculation (wireless optical)
  3. Statistical channel model survey

Statistical channel model

According to [1] the most appropriate channel model for LEO satellites is the mixture of the Rician and lognormal independent fading processes. This channel model also known as Corazza-Vatalaro model or C&V (fig. 1).

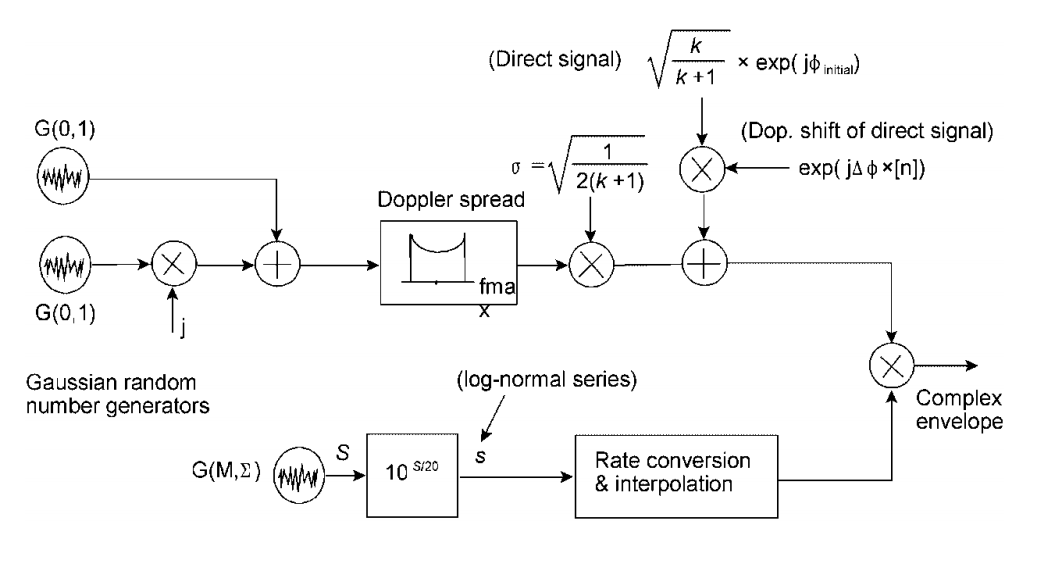Fig. 1. Circuit implementation of the C&V model with Jakes multipath Doppler shaping.[2]

The following variables are used in the upper rail:

  • G(0, 1) is a random variable with a normal (Gaussian) distribution with zero mean and unit variance
  • K is the Rician factor: the ratio between the power of the direct path of electromagnetic wave propagation and the total power of the other paths
  • \phi_{initial} is the initial phase of the direct signal
  • \Delta \phi_{Dir} = 2 \pi f_{Dir}T_s, is the constant phase increment, where T_s is the sampling period, and f_{Dir} is the Doppler shift frequency of the direct path
  • [n] - sample number (x means multiplication)

According to [5, p. 97] Doppler spread block can be modeled via the Butterworth filter (see an example here) with the following parameters:

  • maximum ripple of 3 dB up to 0.9 v_{mobile} / \lambda_c (pass band);
  • attenuation of 100 dB at 3 v_{mobile} / \lambda_c (stop band),

where v_{mobile} is the mobile station velocity, and \lambda_c is the wave length of the carrier.

Lower rail determines slow (large-scaled) fading ("log-normal series"):

  • M - mean of the Gaussian process
  • \Sigma - variance of the Gaussian process

This rail can be reformulated as fig. 2.

Fig. 2. Alternative low-pass filtering method for generating slower varying shadowed signals at the same rate as the multipath rail. [2]

Where:

  • b = \Sigma\sqrt{1 - c^2},
  • c = \exp{\left(-\frac{vT_s}{l_{corr}}\right)},
  • v is the velocity of the mobile terminal, and
  • l_{corr} is the correlation length (3-5 m [4]).

However, special interpolation functions can be also used instead (see an example here)

The multiplication of these rails makes complex envelop of the impulse responce of the considered channel.

Two ultimate conditions are proposed in [1]: light shadowing and strong shadowing (tab.1).

Table 1. Statistical characteristics of the LEO channel

Parameter Light shadowing Strong shadowing
Rician factor (linear scale) 4.0 0.6
Lognormal mean (logarithmic scale) 0.13 -1.08
Lognormal variance (logarithmic scale) 1.0 2.5

Moreover, authors mention that shadowing (lognormal part) is negligible on elevation angles larger than 60 degrees (and smaller than 120 degree) (fig. 3).

params

Fig. 3. Model parameters, sigma, mu and K as a function of the elevation angle, a, in a mal tree-shadowed environment. [1]

Interesting research can be obtained in [5], where both single-state and multi-state models are considered.

Fig. 4. Semi-Markov model for single-satellite reception.[5]

where p_{ij} means the probability of the state changing.

Moreover, the MIMO channel be considered [6-9].

See also:

Two interest frameworks can be considered in case of MIMO channel modeling:

Markov chains based models for dual-satellite systems are also considered in [5].

Markov

Fig. 5. Semi-Markov model for two satellites [5].

The library hmmlearn can be used, for example, for generating of the series for the switching between states.

References

[1] Giovanni E. Corazza and Francesco Vatalaro, A Statistical Model for Land Mobile Satellite Channels and Its Application to Nongeostationary Orbit Systems, Transac- tions on Vehicular Technology, vol. 43, no. 3. August 1994

[2] Fontan, F. P., Mayo, A., Marote, D., Prieto‐Cerdeira, R., Mariño, P., Machado, F., & Riera, N. (2008). Review of generative models for the narrowband land mobile satellite propagation channel. International Journal of Satellite Communications and Networking, 26(4), 291-316.

[3] Loo, C. "Further results on the statistics of propagation data at L-band (1542 MHz) for mobile satellite communications." [1991 Proceedings] 41st IEEE Vehicular Technology Conference. IEEE, 1991.

[4] Perez-Fontan, Fernando, et al. "S-band LMS propagation channel behaviour for different environments, degrees of shadowing and elevation angles." IEEE transactions on broadcasting 44.1 (1998): 40-76.

[5] Arndt, D. (2015). On Channel Modelling for Land Mobile Satellite Reception (Doctoral dissertation).

[6] Arapoglou, P.D.; Liolis, K.; Bertinelli, M.; Panagopoulos, A.; Cottis, P.; De Gaudenzi, R. (2011). "MIMO over satellite: A review". IEEE Communications Surveys & Tutorials. 13 (1): 27–51. doi:10.1109/SURV.2011.033110.00072

[7] Kyröläinen, J.; Hulkkonen, A.; Ylitalo, J.; Byman, A.; Shankar, B.; Arapoglou, P.D.; Grotz, J. (2014). "Applicability of MIMO to satellite communications". International Journal of Satellite Communications and Networking. 32 (4): 343–357. doi:10.1002/sat.1040

[8] Zang, Guo-zhen; Huang Bao-hua; Mu Jing (2010). One scheme of cooperative diversity with two satellites based on the alamouti code. IET 3rd International Conference on Wireless, Mobile and Multimedia Networks (ICWMMN 2010). pp. 151–4. doi:10.1049/cp.2010.0640. ISBN 978-1-84919-240-8.

[9] Pérez-Neira, A.I.; Ibars, C.; Serra, J.; Del Coso, A.; Gómez-Vilardebó, J.; Caus, M.; Liolis, K.P. (2011). "MIMO channel modeling and transmission techniques for multi-satellite and hybrid satellite-terrestrial mobile networks". Physical Communication. 4 (2): 127–139. doi:10.1016/j.phycom.2011.04.001