2467. Most Profitable Path in a Tree

[mah-shamim]

Topics: Array, Tree, Depth-First Search, Breadth-First Search, Graph

There is an undirected tree with n nodes labeled from 0 to n - 1, rooted at node 0. You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

At every node i, there is a gate. You are also given an array of even integers amount, where amount[i] represents:

• the price needed to open the gate at node i, if amount[i] is negative, or,
• the cash reward obtained on opening the gate at node i, otherwise.

The game goes on as follows:

• Initially, Alice is at node 0 and Bob is at node bob.
• At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node 0.
• For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
  • If the gate is already open, no price will be required, nor will there be any cash reward.
  • If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is c, then both Alice and Bob pay c / 2 each. Similarly, if the reward at the gate is c, both of them receive c / 2 each.
• If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node 0, he stops moving. Note that these events are independent of each other.

Return the maximum net income Alice can have if she travels towards the optimal leaf node.

Example 1:

• Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
• Output: 6
• Explanation:
  The above diagram represents the given tree. The game goes as follows:
  • Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes.
    • Alice's net income is now -2.
  • Both Alice and Bob move to node 1.
    • Since they reach here simultaneously, they open the gate together and share the reward.
    • Alice's net income becomes -2 + (4 / 2) = 0.
  • Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged.
    • Bob moves on to node 0, and stops moving.
  • Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6.
    Now, neither Alice nor Bob can make any further moves, and the game ends.
    It is not possible for Alice to get a higher net income.

Example 2:

• Input: edges = [[0,1]], bob = 1, amount = [-7280,2350]
• Output: -7280
• Explanation:
  Alice follows the path 0->1 whereas Bob follows the path 1->0.
  Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280.

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges represents a valid tree.
• 1 <= bob < n
• amount.length == n
• amount[i] is an even integer in the range [-104, 104].

Hint:

1. Bob travels along a fixed path (from node “bob” to node 0).
2. Calculate Alice’s distance to each node via DFS.
3. We can calculate Alice’s score along a path ending at some node easily using Hints 1 and 2.

[mah-shamim]

We need to determine the maximum net income Alice can achieve by traveling from the root node (node 0) to a leaf node in an undirected tree, considering Bob's movement from a given node towards the root. The solution involves calculating the optimal path for Alice while considering the interactions with Bob's path and their respective gate opening times.

Approach

1. Tree Construction: Build an adjacency list from the given edges to represent the tree structure.
2. Parent Tracking: Use BFS to determine the parent of each node, starting from the root node (0). This helps in backtracking Bob's path from his starting node to the root.
3. Bob's Path and Timing: Determine Bob's path from his starting node to the root using the parent pointers and record the time he arrives at each node in his path.
4. DFS for Maximum Profit: Perform a DFS traversal from the root to all leaf nodes, calculating the net income for each path. For each node in Alice's path, compare her arrival time with Bob's to determine the contribution to her net income.

Let's implement this solution in PHP: 2467. Most Profitable Path in a Tree

<?php
/**
 * @param Integer[][] $edges
 * @param Integer $bob
 * @param Integer[] $amount
 * @return Integer
 */
function mostProfitablePath($edges, $bob, $amount) {
    // Build adjacency list
    $adj = [];
    foreach ($edges as $e) {
        $u = $e[0];
        $v = $e[1];
        if (!isset($adj[$u])) $adj[$u] = [];
        if (!isset($adj[$v])) $adj[$v] = [];
        $adj[$u][] = $v;
        $adj[$v][] = $u;
    }

    $n = count($adj);
    $parent = array_fill(0, $n, -1);
    $visited = array_fill(0, $n, false);
    $queue = new SplQueue();
    $queue->enqueue(0);
    $visited[0] = true;

    // BFS to find parent pointers
    while (!$queue->isEmpty()) {
        $u = $queue->dequeue();
        foreach ($adj[$u] as $v) {
            if (!$visited[$v] && $v != $parent[$u]) {
                $parent[$v] = $u;
                $visited[$v] = true;
                $queue->enqueue($v);
            }
        }
    }

    // Get Bob's path and time
    $bob_path = [];
    $current = $bob;
    while ($current != -1) {
        $bob_path[] = $current;
        $current = $parent[$current];
    }

    $bob_time = [];
    $time = 0;
    foreach ($bob_path as $node) {
        $bob_time[$node] = $time++;
    }

    // Iterative DFS to find max sum
    $max_sum = PHP_INT_MIN;
    $stack = [[0, -1, 0, 0]]; // [node, parent, sum, depth]

    while (!empty($stack)) {
        $element = array_pop($stack);
        list($u, $p, $sum, $depth) = $element;

        // Calculate contribution for current node
        if (isset($bob_time[$u])) {
            $alice_time = $depth;
            $b_time = $bob_time[$u];
            if ($alice_time < $b_time) {
                $add_val = $amount[$u];
            } elseif ($alice_time == $b_time) {
                $add_val = $amount[$u] / 2;
            } else {
                $add_val = 0;
            }
        } else {
            $add_val = $amount[$u];
        }

        $new_sum = $sum + $add_val;

        // Check if it's a leaf node
        $is_leaf = ($u != 0) && (count($adj[$u]) == 1);

        if ($is_leaf) {
            if ($new_sum > $max_sum) {
                $max_sum = $new_sum;
            }
        } else {
            // Push children to stack
            foreach ($adj[$u] as $v) {
                if ($v != $p) {
                    array_push($stack, [$v, $u, $new_sum, $depth + 1]);
                }
            }
        }
    }

    return $max_sum;
}

// Example Test Cases
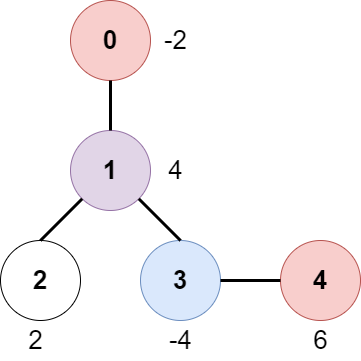
$edges1 = [[0,1],[1,2],[1,3],[3,4]];
$bob1 = 3;
$amount1 = [-2,4,2,-4,6];
echo mostProfitablePath($edges1, $bob1, $amount1) . "\n"; // Output: 6

$edges2 = [[0,1]];
$bob2 = 1;
$amount2 = [-7280,2350];
echo mostProfitablePath($edges2, $bob2, $amount2) . "\n"; // Output: -7280
?>

Explanation:

1. Tree Construction: The adjacency list is built from the given edges to represent the tree structure, allowing efficient traversal.
2. Parent Tracking: BFS is used starting from the root node to determine the parent of each node. This helps in backtracking Bob's path from his starting node to the root.
3. Bob's Path and Timing: By backtracking from Bob's starting node to the root using parent pointers, we determine the time Bob arrives at each node in his path.
4. DFS for Maximum Profit: Using iterative DFS, we traverse from the root to all leaf nodes. For each node, we calculate Alice's net income considering her arrival time relative to Bob's. The maximum net income encountered during the traversal is returned as the result.

This approach efficiently handles the tree traversal and timing comparisons to determine the optimal path for Alice, ensuring the solution is both correct and performant for large trees.

[kovatz]

Thanks for solving the problem of "Most Profitable Path in a Tree"

[mah-shamim]

Thanks