2685. Count the Number of Complete Components #1465
-
|
Topics: You are given an integer Return the number of complete connected components of the graph. A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph. A connected component is said to be complete if there exists an edge between every pair of its vertices. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to count the number of complete connected components in an undirected graph. A complete connected component is one where every pair of vertices is connected by an edge. Approach
Let's implement this solution in PHP: 2685. Count the Number of Complete Components <?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @return Integer
*/
function countCompleteComponents($n, $edges) {
$adj = array_fill(0, $n, array());
$edgeSet = array();
foreach ($edges as $e) {
$a = $e[0];
$b = $e[1];
$adj[$a][] = $b;
$adj[$b][] = $a;
$sorted = [min($a, $b), max($a, $b)];
$edgeSet[implode(',', $sorted)] = true;
}
$visited = array_fill(0, $n, false);
$result = 0;
for ($i = 0; $i < $n; $i++) {
if (!$visited[$i]) {
$component = array();
$queue = array();
array_push($queue, $i);
$visited[$i] = true;
$component[] = $i;
while (!empty($queue)) {
$node = array_shift($queue);
foreach ($adj[$node] as $neighbor) {
if (!$visited[$neighbor]) {
$visited[$neighbor] = true;
array_push($queue, $neighbor);
$component[] = $neighbor;
}
}
}
$m = count($component);
if ($m == 1) {
$result++;
continue;
}
$required = $m * ($m - 1) / 2;
$actual = 0;
for ($j = 0; $j < $m; $j++) {
for ($k = $j + 1; $k < $m; $k++) {
$u = $component[$j];
$v = $component[$k];
$key = min($u, $v) . ',' . max($u, $v);
if (isset($edgeSet[$key])) {
$actual++;
}
}
}
if ($actual == $required) {
$result++;
}
}
}
return $result;
}
// Example usage:
$n = 6;
$edges = [[0,1],[0,2],[1,2],[3,4]];
echo countCompleteComponents($n, $edges); // Output: 3
$n2 = 6;
$edges2 = [[0,1],[0,2],[1,2],[3,4],[3,5]];
echo countCompleteComponents($n2, $edges2); // Output: 1
?>Explanation:
This approach efficiently identifies and checks each connected component, ensuring the solution is both correct and optimal for the given problem constraints. |
Beta Was this translation helpful? Give feedback.
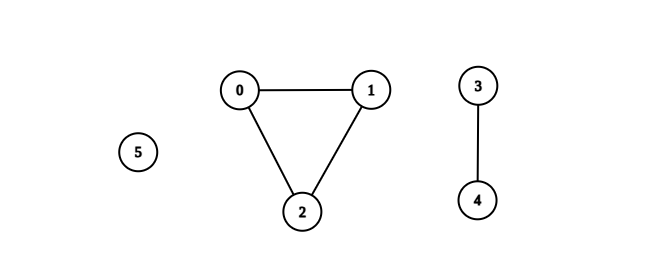
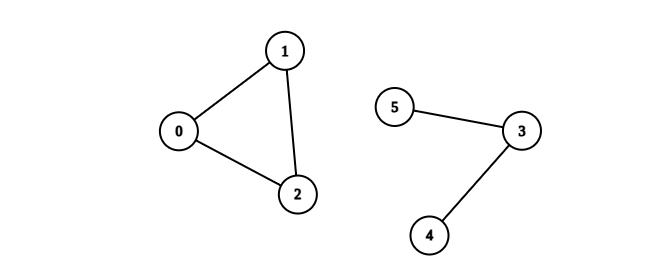
We need to count the number of complete connected components in an undirected graph. A complete connected component is one where every pair of vertices is connected by an edge.
Approach
mnodes is…