1976. Number of Ways to Arrive at Destination #1469
-
|
Topics: You are in a city that consists of You are given an integer Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to determine the number of ways to travel from intersection 0 to intersection n-1 in the shortest possible time using bidirectional roads. The solution involves using Dijkstra's algorithm to find the shortest paths and then dynamic programming (DP) to count the number of ways to reach the destination using those shortest paths. Approach
Let's implement this solution in PHP: 1976. Number of Ways to Arrive at Destination <?php
/**
* @param Integer $n
* @param Integer[][] $roads
* @return Integer
*/
function countPaths($n, $roads) {
if ($n == 1) return 1;
$mod = 1000000007;
// Build adjacency list for Dijkstra's algorithm
$adj = array_fill(0, $n, array());
foreach ($roads as $road) {
$u = $road[0];
$v = $road[1];
$t = $road[2];
$adj[$u][] = array($v, $t);
$adj[$v][] = array($u, $t);
}
// Dijkstra's algorithm to find shortest distances from node 0
$dist = array_fill(0, $n, PHP_INT_MAX);
$dist[0] = 0;
$pq = new SplPriorityQueue();
$pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);
$pq->insert(array(0, 0), -0);
while (!$pq->isEmpty()) {
$elem = $pq->extract();
$currentDist = -$elem['priority'];
$u = $elem['data'][1];
if ($currentDist > $dist[$u]) continue;
foreach ($adj[$u] as $edge) {
$v = $edge[0];
$t = $edge[1];
$newDist = $currentDist + $t;
if ($newDist < $dist[$v]) {
$dist[$v] = $newDist;
$pq->insert(array($newDist, $v), -$newDist);
}
}
}
// Build the DAG adjacency list
$dagAdj = array_fill(0, $n, array());
foreach ($roads as $road) {
$u = $road[0];
$v = $road[1];
$t = $road[2];
if ($dist[$u] + $t == $dist[$v]) {
$dagAdj[$u][] = $v;
}
if ($dist[$v] + $t == $dist[$u]) {
$dagAdj[$v][] = $u;
}
}
// Sort nodes based on their distance from 0
$nodes = range(0, $n-1);
usort($nodes, function ($a, $b) use ($dist) {
return $dist[$a] - $dist[$b];
});
// Dynamic programming to count paths
$dp = array_fill(0, $n, 0);
$dp[0] = 1;
foreach ($nodes as $u) {
foreach ($dagAdj[$u] as $v) {
$dp[$v] = ($dp[$v] + $dp[$u]) % $mod;
}
}
return $dp[$n-1] % $mod;
}
// Example Test Cases
$n1 = 7;
$roads1 = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]];
echo countPaths($n1, $roads1) . "\n"; // Output: 4
$n2 = 2;
$roads2 = [[1,0,10]];
echo countPaths($n2, $roads2) . "\n"; // Output: 1
?>Explanation:
This approach efficiently combines graph traversal and dynamic programming to solve the problem within the constraints. |
Beta Was this translation helpful? Give feedback.
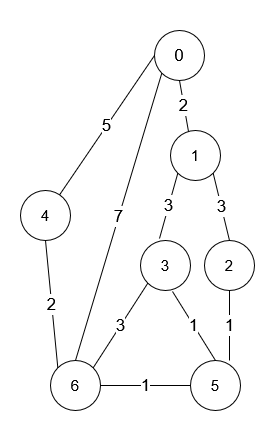
We need to determine the number of ways to travel from intersection 0 to intersection n-1 in the shortest possible time using bidirectional roads. The solution involves using Dijkstra's algorithm to find the shortest paths and then dynamic programming (DP) to count the number of ways to reach the destination using those shortest paths.
Approach