3394. Check if Grid can be Cut into Sections #1477
-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to determine if we can make two horizontal or vertical cuts on an n x n grid such that the grid is divided into three sections, each containing at least one rectangle without any overlap. The approach involves checking both horizontal and vertical directions to see if such cuts are possible. Approach
Let's implement this solution in PHP: 3394. Check if Grid can be Cut into Sections <?php
/**
* @param Integer $n
* @param Integer[][] $rectangles
* @return Boolean
*/
function checkValidCuts($n, $rectangles) {
$xs = array();
$ys = array();
foreach ($rectangles as $rect) {
$startX = $rect[0];
$startY = $rect[1];
$endX = $rect[2];
$endY = $rect[3];
array_push($xs, array($startX, $endX));
array_push($ys, array($startY, $endY));
}
$countX = countMerged($xs);
$countY = countMerged($ys);
return max($countX, $countY) >= 3;
}
/**
* @param $intervals
* @return int
*/
private function countMerged($intervals) {
$count = 0;
$prevEnd = 0;
usort($intervals, function($a, $b) {
if ($a[0] < $b[0]) {
return -1;
} elseif ($a[0] > $b[0]) {
return 1;
} else {
return 0;
}
});
foreach ($intervals as $interval) {
$start = $interval[0];
$end = $interval[1];
if ($start < $prevEnd) {
$prevEnd = max($prevEnd, $end);
} else {
$prevEnd = $end;
$count++;
}
}
return $count;
}
// Example Test Cases
$n1 = 5;
$rectangles1 = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]];
echo checkValidCuts($n1, $rectangles1) ? 'true' : 'false'; // Output: true
$n2 = 4;
$rectangles2 = [[0,0,1,1],[2,0,3,4],[0,2,2,3],[3,0,4,3]];
echo "\n" . (checkValidCuts($n2, $rectangles2) ? 'true' : 'false'); // Output: true
$n3 = 4;
$rectangles3 = [[0,2,2,4],[1,0,3,2],[2,2,3,4],[3,0,4,2],[3,2,4,4]];
echo "\n" . (checkValidCuts($n3, $rectangles3) ? 'true' : 'false'); // Output: false
?>Explanation:
This approach efficiently checks both directions and leverages interval merging to determine the feasibility of the required cuts. The solution runs in O(n log n) time due to sorting and merging intervals, which is efficient given the problem constraints. |
Beta Was this translation helpful? Give feedback.
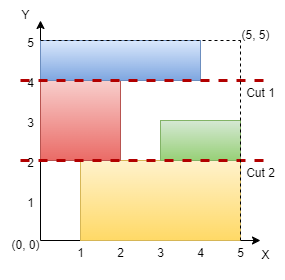
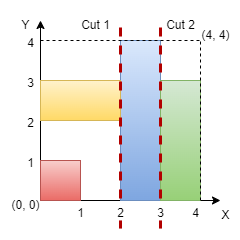
We need to determine if we can make two horizontal or vertical cuts on an n x n grid such that the grid is divided into three sections, each containing at least one rectangle without any overlap. The approach involves checking both horizontal and vertical directions to see if such cuts are possible.
Approach