1123. Lowest Common Ancestor of Deepest Leaves #1517
-
|
Topics: Given the Recall that:
Example 1:
Example 2:
Example 3:
Constraints:
Note: This question is the same as 865. Smallest Subtree with all the Deepest Nodes Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to find the lowest common ancestor (LCA) of the deepest leaves in a binary tree. The LCA of a set of nodes is the node with the largest depth such that every node in the set is in the subtree rooted at this node. The deepest leaves are the leaves at the maximum depth in the tree. ApproachThe approach involves a post-order traversal of the tree. For each node, we compute the maximum depth of its left and right subtrees. If both subtrees have the same maximum depth, the current node is the LCA of the deepest leaves in its subtree. Otherwise, the LCA is derived from the subtree with the greater depth. This approach ensures that we efficiently determine the LCA without explicitly collecting all deepest leaves and then computing their LCA. Let's implement this solution in PHP: 1123. Lowest Common Ancestor of Deepest Leaves <?php
/**
* @param TreeNode $root
* @return TreeNode
*/
function lcaDeepestLeaves($root) {
$result = dfs($root, 0);
return $result[1];
}
/**
* @param $node
* @param $depth
* @return array
*/
function dfs($node, $depth) {
if ($node === null) {
return [-INF, null];
}
if ($node->left === null && $node->right === null) {
return [$depth, $node];
}
$left = $this->dfs($node->left, $depth + 1);
$right = $this->dfs($node->right, $depth + 1);
if ($left[0] > $right[0]) {
return [$left[0], $left[1]];
} elseif ($right[0] > $left[0]) {
return [$right[0], $right[1]];
} else {
return [$left[0], $node];
}
}
// Test Cases
$testCases = [
// Test Case 1
[
'input' => [3, 5, 1, 6, 2, 0, 8, null, null, 7, 4],
'expected' => 2
],
// Test Case 2
[
'input' => [1],
'expected' => 1
],
// Test Case 3
[
'input' => [0, 1, 3, null, 2],
'expected' => 2
],
// Test Case 4: Edge Case with one node
[
'input' => [10],
'expected' => 10
],
// Test Case 5: Larger tree with deeper leaves
[
'input' => [1, 2, 3, 4, 5, 6, 7, null, null, 8, 9],
'expected' => 8
],
];
foreach ($testCases as $index => $testCase) {
$input = $testCase['input'];
$expected = $testCase['expected'];
// Build the tree from the array
$tree = buildTree($input);
$result = lcaDeepestLeaves($tree);
// Output the result
echo "Test Case " . ($index + 1) . ":\n";
echo "Input: " . implode(",", $input) . "\n";
echo "Expected Output: " . $expected . "\n";
echo "Output: " . $result->val . "\n\n";
}
//Output
Test Case 1:
Input: 3,5,1,6,2,0,8,,,
Expected Output: 2
Output: 2
Test Case 2:
Input: 1
Expected Output: 1
Output: 1
Test Case 3:
Input: 0,1,3,,2
Expected Output: 2
Output: 2
Test Case 4:
Input: 10
Expected Output: 10
Output: 10
Test Case 5:
Input: 1,2,3,4,5,6,7,,,8,9
Expected Output: 8
Output: 8
?>Explanation:
This approach efficiently computes the LCA in O(n) time complexity, where n is the number of nodes in the tree, as each node is visited exactly once. The space complexity is O(h) due to the recursion stack, where h is the height of the tree. |
Beta Was this translation helpful? Give feedback.
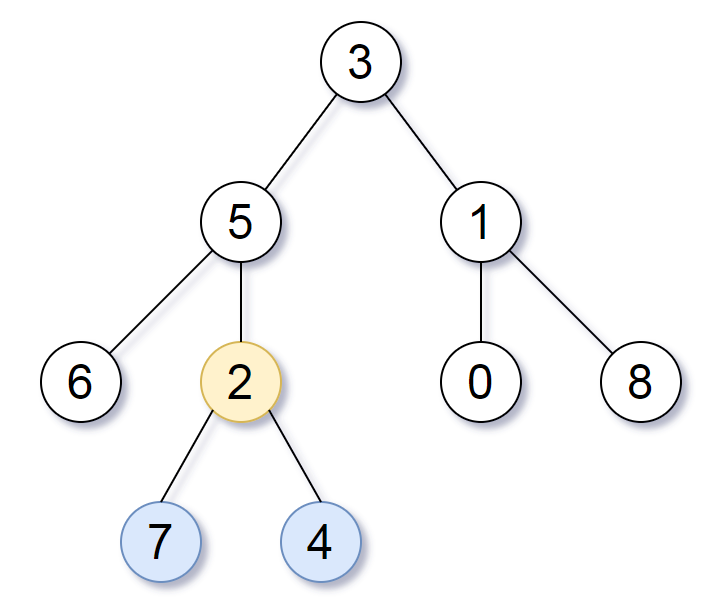
We need to find the lowest common ancestor (LCA) of the deepest leaves in a binary tree. The LCA of a set of nodes is the node with the largest depth such that every node in the set is in the subtree rooted at this node. The deepest leaves are the leaves at the maximum depth in the tree.
Approach
The approach involves a post-order traversal of the tree. For each node, we compute the maximum depth of its left and right subtrees. If both subtrees have the same maximum depth, the current node is the LCA of the deepest leaves in its subtree. Otherwise, the LCA is derived from the subtree with the greater depth. This approach ensures that we efficiently determine the LCA without explicitly col…