790. Domino and Tromino Tiling #1646
-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to determine the number of ways to tile a 2xN board using dominoes and trominoes. The solution involves dynamic programming to efficiently compute the number of valid tilings. ApproachThe key insight is to recognize the recurrence relation that captures the number of ways to tile the board up to a given length. The recurrence relation is derived based on the different ways tiles can be added to extend the tiling from smaller boards to larger ones. The recurrence relation is:
This relation accounts for:
Let's implement this solution in PHP: 790. Domino and Tromino Tiling <?php
/**
* @param Integer $n
* @return Integer
*/
function numTilings($n) {
$mod = 1000000007;
if ($n == 0) return 1;
if ($n == 1) return 1;
if ($n == 2) return 2;
$dp = array_fill(0, $n + 1, 0);
$dp[0] = 1;
$dp[1] = 1;
$dp[2] = 2;
for ($i = 3; $i <= $n; $i++) {
$dp[$i] = (2 * $dp[$i - 1] + $dp[$i - 3]) % $mod;
}
return $dp[$n];
}
// Example usage
echo numTilings(3); // Output: 5
echo numTilings(1); // Output: 1
echo numTilings(2); // Output: 2
echo numTilings(4); // Output: 11
echo numTilings(5) // Output: 24
?>Explanation:
This approach efficiently computes the number of tilings using dynamic programming, ensuring optimal time complexity of O(n) and space complexity of O(n). |
Beta Was this translation helpful? Give feedback.
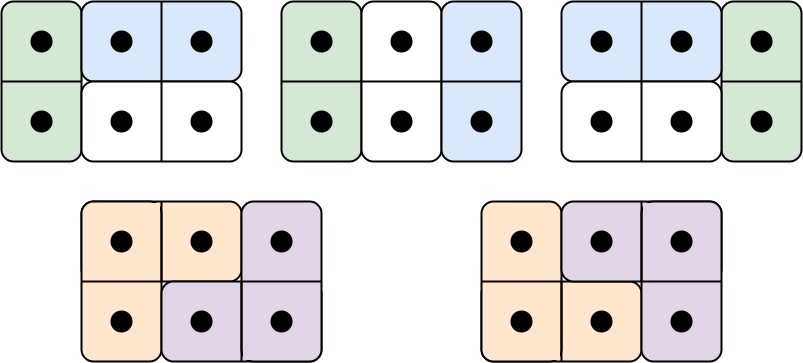
We need to determine the number of ways to tile a 2xN board using dominoes and trominoes. The solution involves dynamic programming to efficiently compute the number of valid tilings.
Approach
The key insight is to recognize the recurrence relation that captures the number of ways to tile the board up to a given length. The recurrence relation is derived based on the different ways tiles can be added to extend the tiling from smaller boards to larger ones. The recurrence relation is:
dp[n] = 2 * dp[n-1] + dp[n-3]This relation accounts for:
n-1.n-2.