3372. Maximize the Number of Target Nodes After Connecting Trees I #1738
-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to maximize the number of target nodes for each node in the first tree after connecting it to a node in the second tree. A target node for a given node is any node within a distance of at most Approach
Let's implement this solution in PHP: 3372. Maximize the Number of Target Nodes After Connecting Trees I <?php
/**
* @param Integer[][] $edges1
* @param Integer[][] $edges2
* @param Integer $k
* @return Integer[]
*/
function maxTargetNodes($edges1, $edges2, $k) {
$n = count($edges1) + 1;
$m = count($edges2) + 1;
$graph1 = array_fill(0, $n, array());
foreach ($edges1 as $edge) {
$a = $edge[0];
$b = $edge[1];
$graph1[$a][] = $b;
$graph1[$b][] = $a;
}
$count1_arr = array_fill(0, $n, 0);
for ($i = 0; $i < $n; $i++) {
$dist = array_fill(0, $n, -1);
$q = array_fill(0, $n, 0);
$head = 0;
$tail = 0;
$dist[$i] = 0;
$q[$tail++] = $i;
$cnt = 1;
while ($head < $tail) {
$u = $q[$head++];
foreach ($graph1[$u] as $v) {
if ($dist[$v] == -1) {
$nd = $dist[$u] + 1;
if ($nd <= $k) {
$dist[$v] = $nd;
$cnt++;
$q[$tail++] = $v;
}
}
}
}
$count1_arr[$i] = $cnt;
}
$M = 0;
if ($k - 1 >= 0) {
$graph2 = array_fill(0, $m, array());
foreach ($edges2 as $edge) {
$u = $edge[0];
$v = $edge[1];
$graph2[$u][] = $v;
$graph2[$v][] = $u;
}
for ($j = 0; $j < $m; $j++) {
$dist = array_fill(0, $m, -1);
$q = array_fill(0, $m, 0);
$head = 0;
$tail = 0;
$dist[$j] = 0;
$q[$tail++] = $j;
$cnt = 1;
while ($head < $tail) {
$u = $q[$head++];
foreach ($graph2[$u] as $v) {
if ($dist[$v] == -1) {
$nd = $dist[$u] + 1;
if ($nd <= $k - 1) {
$dist[$v] = $nd;
$cnt++;
$q[$tail++] = $v;
}
}
}
}
if ($cnt > $M) {
$M = $cnt;
}
}
}
$ans = array();
for ($i = 0; $i < $n; $i++) {
$ans[] = $count1_arr[$i] + $M;
}
return $ans;
}
// Example 1
$edges1 = [[0,1],[0,2],[2,3],[2,4]];
$edges2 = [[0,1],[0,2],[0,3],[2,7],[1,4],[4,5],[4,6]];
$k = 2;
print_r(maxTargetNodes($edges1, $edges2, $k)); // [9,7,9,8,8]
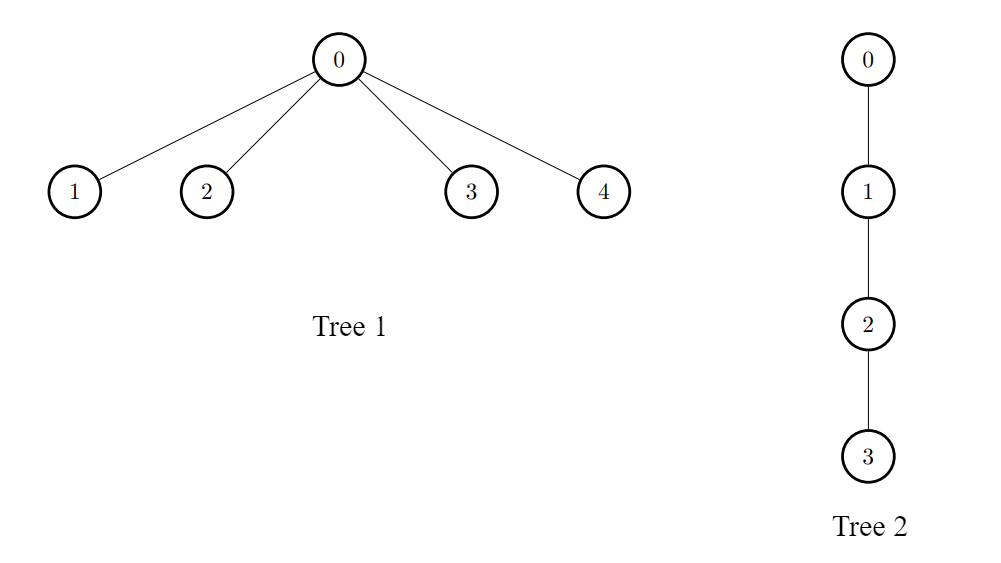
// Example 2
$edges1 = [[0,1],[0,2],[0,3],[0,4]];
$edges2 = [[0,1],[1,2],[2,3]];
$k = 1;
print_r(maxTargetNodes($edges1, $edges2, $k)); // [6,3,3,3,3]
?>Explanation:
This approach efficiently computes the solution by leveraging BFS for distance-based counts and combines results from both trees to maximize the target nodes for each query. The complexity is manageable within the problem constraints. |
Beta Was this translation helpful? Give feedback.
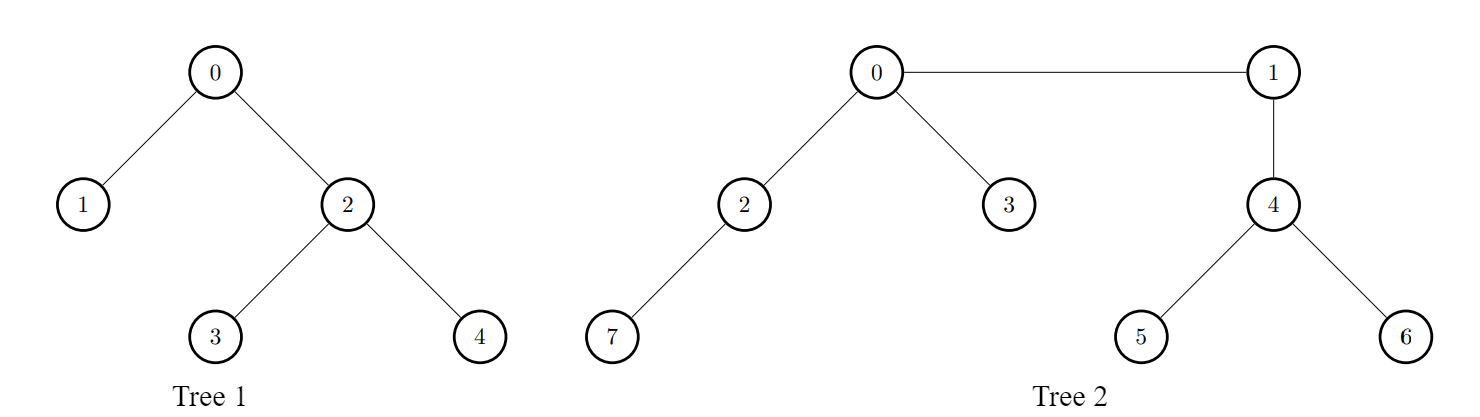
We need to maximize the number of target nodes for each node in the first tree after connecting it to a node in the second tree. A target node for a given node is any node within a distance of at most
kfrom it. The solution involves efficiently calculating the number of nodes within the specified distance in both trees and then combining these counts optimally.Approach
Problem Analysis: The problem requires us to compute, for each node in the first tree, the maximum number of target nodes achievable by connecting it to any node in the second tree. The target nodes include nodes from both trees that are within a distance
kfrom the node in the first tree. The connection between the tre…