2359. Find Closest Node to Given Two Nodes #1746
-
|
Topics: You are given a directed graph of The graph is represented with a given 0-indexed array You are also given two integers Return the index of the node that can be reached from both Note that Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to find the closest node in a directed graph that is reachable from two given nodes, Approach
Let's implement this solution in PHP: 2359. Find Closest Node to Given Two Nodes <?php
/**
* @param Integer[] $edges
* @param Integer $node1
* @param Integer $node2
* @return Integer
*/
function closestMeetingNode($edges, $node1, $node2) {
$n = count($edges);
$dist1 = array_fill(0, $n, -1);
$dist2 = array_fill(0, $n, -1);
$cur = $node1;
$step = 0;
while ($cur != -1 && $dist1[$cur] == -1) {
$dist1[$cur] = $step;
$step++;
$cur = $edges[$cur];
}
$cur = $node2;
$step = 0;
while ($cur != -1 && $dist2[$cur] == -1) {
$dist2[$cur] = $step;
$step++;
$cur = $edges[$cur];
}
$minMax = PHP_INT_MAX;
$ans = -1;
for ($i = 0; $i < $n; $i++) {
if ($dist1[$i] == -1 || $dist2[$i] == -1) {
continue;
}
$maxDist = max($dist1[$i], $dist2[$i]);
if ($maxDist < $minMax) {
$minMax = $maxDist;
$ans = $i;
}
}
return $ans;
}
// Example 1
$edges = [2, 2, 3, -1];
$node1 = 0;
$node2 = 1;
echo closestMeetingNode($edges, $node1, $node2) . "\n"; // Output: 2
// Example 2
$edges = [1, 2, -1];
$node1 = 0;
$node2 = 2;
echo closestMeetingNode($edges, $node1, $node2) . "\n"; // Output: 2
?>Explanation:
This approach efficiently leverages the graph's deterministic structure to compute distances and find the optimal meeting node with minimal computational overhead. |
Beta Was this translation helpful? Give feedback.
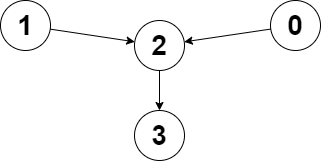
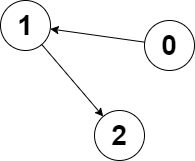
We need to find the closest node in a directed graph that is reachable from two given nodes,
node1andnode2, such that the maximum of the distances fromnode1andnode2to this node is minimized. If multiple nodes satisfy this condition, we return the smallest index among them. If no such node exists, we return-1.Approach
node1andnode2that minimizes the maximum of their distances to this node.