834. Sum of Distances in Tree #188
-
|
Topics: There is an undirected connected tree with You are given the integer Return an array Example 1:
Example 2:
Example 3:
Constraints:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We use a combination of Depth-First Search (DFS) and dynamic programming techniques. The goal is to efficiently compute the sum of distances for each node in a tree with Approach:
Detailed Steps:
Let's implement this solution in PHP: 834. Sum of Distances in Tree <?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @return Integer[]
*/
function sumOfDistancesInTree($n, $edges) {
// Build adjacency list
$g = array_fill(0, $n, array());
foreach ($edges as $e) {
$a = $e[0];
$b = $e[1];
$g[$a][] = $b;
$g[$b][] = $a;
}
// Arrays to store answers, subtree sizes, and visit status
$ans = array_fill(0, $n, 0);
$size = array_fill(0, $n, 0);
// First DFS to calculate the size of each subtree and the distance for root
$dfs1 = function ($i, $fa, $d) use (&$ans, &$size, &$g, &$dfs1) {
$ans[0] += $d;
$size[$i] = 1;
foreach ($g[$i] as $j) {
if ($j != $fa) {
$dfs1($j, $i, $d + 1);
$size[$i] += $size[$j];
}
}
};
// Second DFS to calculate the distance for all nodes
$dfs2 = function ($i, $fa, $t) use (&$ans, &$size, &$g, &$dfs2, $n) {
$ans[$i] = $t;
foreach ($g[$i] as $j) {
if ($j != $fa) {
$dfs2($j, $i, $t - $size[$j] + ($n - $size[$j]));
}
}
};
// Run the first DFS from node 0
$dfs1(0, -1, 0);
// Run the second DFS from node 0 with initial total distance
$dfs2(0, -1, $ans[0]);
return $ans;
}
// Example usage
$n1 = 6;
$edges1 = [[0,1],[0,2],[2,3],[2,4],[2,5]];
print_r(sumOfDistancesInTree($n1, $edges1)); // Output: [8,12,6,10,10,10]
$n2 = 1;
$edges2 = [];
print_r(sumOfDistancesInTree($n2, $edges2)); // Output: [0]
$n3 = 2;
$edges3 = [[1,0]];
print_r(sumOfDistancesInTree($n3, $edges3)); // Output: [1,1]
?>Explanation:
This approach efficiently computes the required distances using two DFS traversals, achieving a time complexity of |
Beta Was this translation helpful? Give feedback.
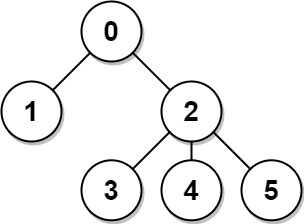

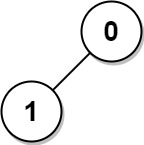
We use a combination of Depth-First Search (DFS) and dynamic programming techniques. The goal is to efficiently compute the sum of distances for each node in a tree with
nnodes andn-1edges.Approach:
dfs1):dfs2):Detailed Steps: