1518. Water Bottles

[mah-shamim]

Topics: Math, Simulation

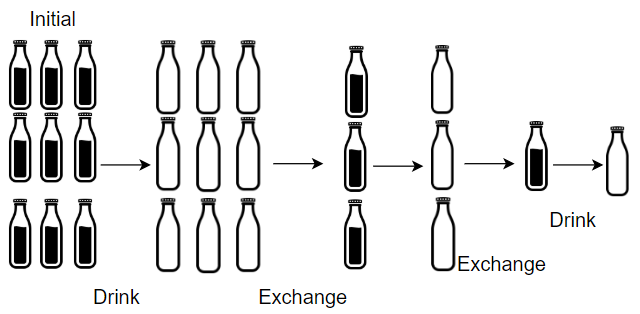
There are numBottles water bottles that are initially full of water. You can exchange numExchange empty water bottles from the market with one full water bottle.

The operation of drinking a full water bottle turns it into an empty bottle.

Given the two integers numBottles and numExchange, return the maximum number of water bottles you can drink.

Example 1:

• Input: numBottles = 9, numExchange = 3
• Output: 13
• Explanation: You can exchange 3 empty bottles to get 1 full water bottle.
  Number of water bottles you can drink: 9 + 3 + 1 = 13.

Example 2:

• Input: numBottles = 15, numExchange = 4
• Output: 19
• Explanation: You can exchange 4 empty bottles to get 1 full water bottle.
  Number of water bottles you can drink: 15 + 3 + 1 = 19.

Constraints:

• 1 <= numBottles <= 100.
• 2 <= numExchange <= 100

Hint:

1. Simulate the process until there are not enough empty bottles for even one full bottle of water.

[mah-shamim]

The problem is to maximize the number of water bottles that can be consumed, given a starting number of full water bottles (numBottles) and an exchange rate (numExchange). Each time you drink a full bottle, it becomes an empty bottle. Once you have enough empty bottles (equal to numExchange), you can trade them for full bottles. The goal is to compute how many total water bottles you can drink, including those obtained through exchanges.

Key Points

• You start with a certain number of full bottles.
• Drinking one full bottle turns it into an empty bottle.
• You can trade a specific number of empty bottles (numExchange) for one full bottle.
• The task is to maximize the total number of bottles drunk.

Approach

To solve this, we can simulate the process:

1. Drink all the full bottles you currently have.
2. Collect the empty bottles from the ones you drank.
3. If you have enough empty bottles, exchange them for new full bottles.
4. Continue this process until you can no longer exchange empty bottles for full ones.

The key challenge is to keep track of the full and empty bottles and handle the exchange process effectively.

Plan

1. Initialize totalDrunk to 0 to keep track of the number of bottles you've drunk.
2. Initialize emptyBottles to 0 to track the number of empty bottles you've accumulated.
3. Start a loop while there are still full bottles:

• Drink all the full bottles, and increase totalDrunk.
• Convert those bottles into empty bottles and add to emptyBottles.
• If you have enough empty bottles (emptyBottles >= numExchange), exchange them for new full bottles.

4. Return totalDrunk as the final answer.

Let's implement this solution in PHP: 1518. Water Bottles

<?php
/**
 * @param Integer $numBottles
 * @param Integer $numExchange
 * @return Integer
 */
function numWaterBottles($numBottles, $numExchange) {
    $totalDrunk = 0;
    $emptyBottles = 0;

    while ($numBottles > 0) {
        // Drink all the current full bottles
        $totalDrunk += $numBottles;

        // Collect the empty bottles
        $emptyBottles += $numBottles;

        // Exchange the empty bottles for new full ones
        $numBottles = floor($emptyBottles / $numExchange);
        $emptyBottles = $emptyBottles % $numExchange;
    }

    return $totalDrunk;
}

// Example usage:
$numBottles = 9;
$numExchange = 3;
echo numWaterBottles($numBottles, $numExchange) . "\n"; // Output: 13

$numBottles = 15;
$numExchange = 4;
echo numWaterBottles($numBottles, $numExchange) . "\n"; // Output: 19
?>

Explanation:

1. Initial Setup: You start with a certain number of full bottles (numBottles), and at the beginning, no empty bottles.
2. Drinking the Bottles: Every time you drink a bottle, it counts towards the totalDrunk and becomes an empty bottle.
3. Exchanging Empty Bottles: If you have enough empty bottles (emptyBottles >= numExchange), you exchange them for full bottles.
4. Repeat: Continue the process until there are not enough empty bottles to exchange for a full one.

Example Walkthrough

Example 1:

• Input: numBottles = 9, numExchange = 3
• Process:
  • Drink all 9 full bottles → totalDrunk = 9, emptyBottles = 9.
  • Exchange 9 empty bottles for 3 full bottles → numBottles = 3, emptyBottles = 0.
  • Drink the 3 full bottles → totalDrunk = 12, emptyBottles = 3.
  • Exchange 3 empty bottles for 1 full bottle → numBottles = 1, emptyBottles = 0.
  • Drink the 1 full bottle → totalDrunk = 13, emptyBottles = 1.
  • No more full bottles to exchange. End.
• Output: 13

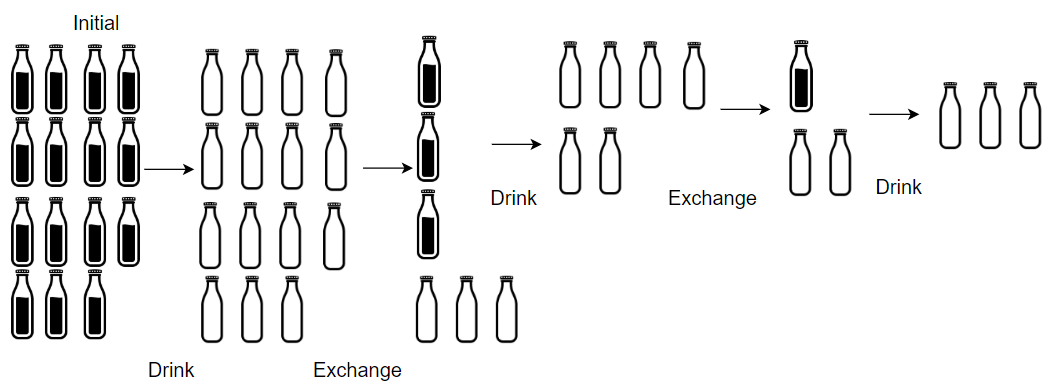
Example 2:

• Input: numBottles = 15, numExchange = 4
• Process:
  • Drink all 15 full bottles → totalDrunk = 15, emptyBottles = 15.
  • Exchange 15 empty bottles for 3 full bottles → numBottles = 3, emptyBottles = 3.
  • Drink the 3 full bottles → totalDrunk = 18, emptyBottles = 6.
  • Exchange 6 empty bottles for 1 full bottle → numBottles = 1, emptyBottles = 2.
  • Drink the 1 full bottle → totalDrunk = 19, emptyBottles = 3.
  • No more full bottles to exchange. End.
• Output: 19

Time Complexity

• Time Complexity: O(numBottles) because each loop iteration consumes a fixed number of bottles and reduces the total number of bottles or empty bottles.
• Space Complexity: O(1) since we only use a constant amount of extra space.

Output for Example

Example 1:

• Input: numBottles = 9, numExchange = 3
• Output: 13

Example 2:

• Input: numBottles = 15, numExchange = 4
• Output: 19

The problem can be solved efficiently by simulating the exchange process and keeping track of full and empty bottles. This approach ensures we maximize the total number of bottles drunk while following the exchange rules. The solution is both time-efficient and space-efficient, making it well-suited for the given constraints.

[basharul-siddike]

Thanks for solving the problem of "Water Bottles"

[mah-shamim]

Thanks