2471. Minimum Number of Operations to Sort a Binary Tree by Level #990
-
|
Topics: You are given the In one operation, you can choose any two nodes at the same level and swap their values. Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order. The level of a node is the number of edges along the path between it and the root node. Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
The problem is about sorting the values of a binary tree level by level in strictly increasing order with the minimum number of operations. In each operation, we can swap the values of two nodes that are at the same level. The goal is to determine the minimum number of such operations required to achieve the sorted order. Key Points:
Approach:
Plan:
Let's implement this solution in PHP: 2471. Minimum Number of Operations to Sort a Binary Tree by Level <?php
/**
* @param TreeNode $root
* @return Integer
*/
function minimumOperations($root) {
if (!$root) {
return 0;
}
// Step 1: Perform BFS to get nodes at each level
$levels = [];
$queue = [[$root, 0]]; // Node and level
while (!empty($queue)) {
list($node, $level) = array_shift($queue);
if (!isset($levels[$level])) {
$levels[$level] = [];
}
$levels[$level][] = $node->val;
if ($node->left) {
$queue[] = [$node->left, $level + 1];
}
if ($node->right) {
$queue[] = [$node->right, $level + 1];
}
}
// Step 2: Calculate the minimum swaps for each level
$totalSwaps = 0;
foreach ($levels as $level) {
$totalSwaps += $this->minSwapsToSort($level);
}
return $totalSwaps;
}
/**
* Function to calculate minimum swaps to sort an array
*
* @param $arr
* @return int
*/
function minSwapsToSort($arr) {
$n = count($arr);
$sortedArr = $arr;
sort($sortedArr);
$indexMap = array_flip($arr);
$visited = array_fill(0, $n, false);
$swaps = 0;
for ($i = 0; $i < $n; $i++) {
if ($visited[$i] || $sortedArr[$i] == $arr[$i]) {
continue;
}
$cycleSize = 0;
$x = $i;
while (!$visited[$x]) {
$visited[$x] = true;
$cycleSize++;
$x = $indexMap[$sortedArr[$x]];
}
if ($cycleSize > 1) {
$swaps += $cycleSize - 1;
}
}
return $swaps;
}
?>Explanation:
Example Walkthrough:Example 1:Input tree: Levels:
Total swaps = 1 (Level 1) + 2 (Level 2) = 3 swaps. Output: 3 Example 2:Input tree: Levels:
Total swaps = 1 (Level 1) + 2 (Level 2) = 3 swaps. Output: 3 Time Complexity:
Thus, the overall time complexity is O(N log N), which is efficient enough given the constraints. Output for Example:For the input tree: The output is This solution efficiently calculates the minimum number of swaps needed to sort each level of the binary tree by using BFS to group nodes by level and cycle decomposition to minimize the number of swaps. The time complexity of O(N log N) is optimal for handling trees with up to 10^5 nodes. |
Beta Was this translation helpful? Give feedback.
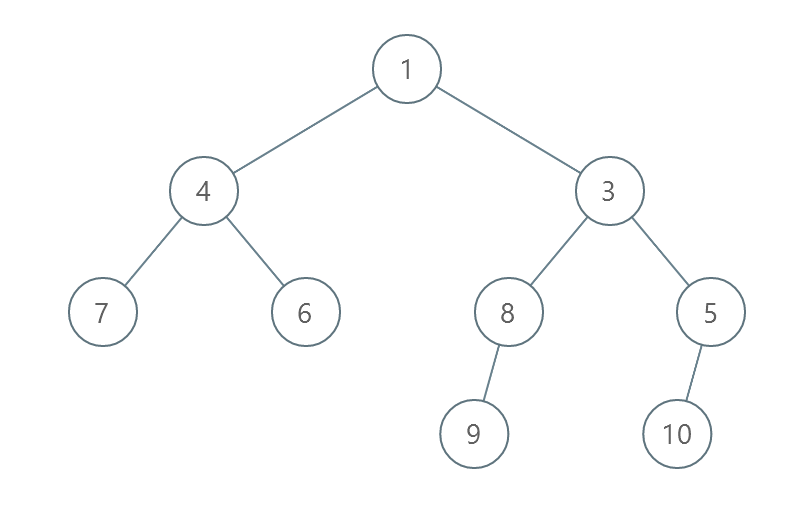
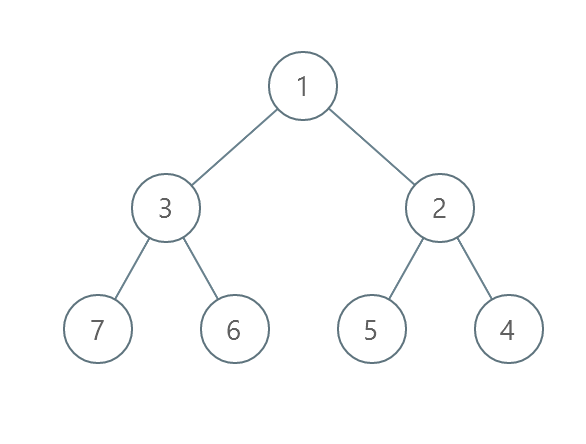
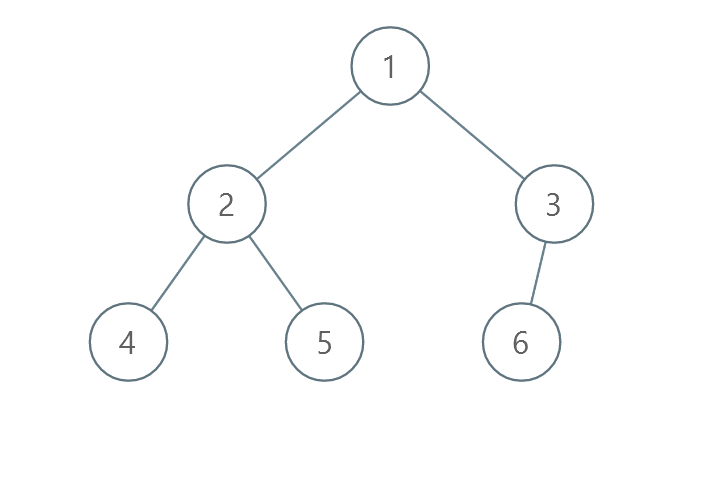
The problem is about sorting the values of a binary tree level by level in strictly increasing order with the minimum number of operations. In each operation, we can swap the values of two nodes that are at the same level. The goal is to determine the minimum number of such operations required to achieve the sorted order.
Key Points: